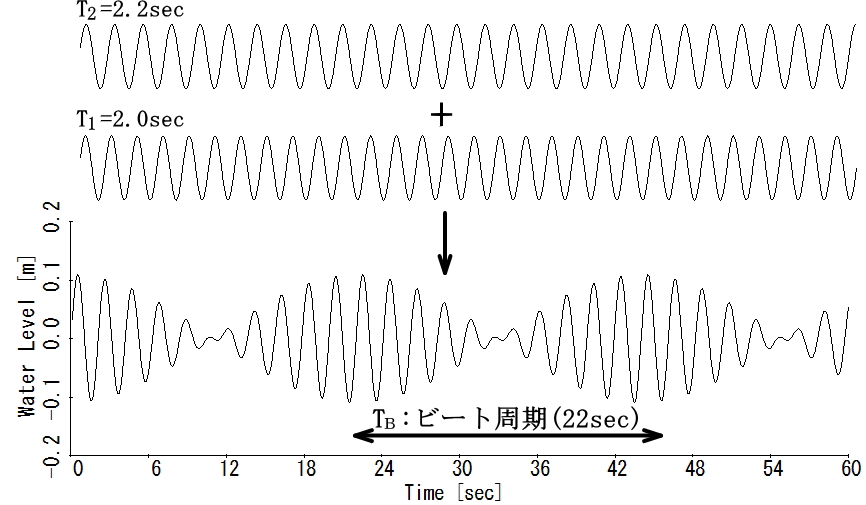
周期がわずかに異なる規則波が重なると合成波の振幅が周期的に大きくなっ
たり小さくなったりする。この様な現象をうなり(Beat)と言う。2つの規則波
を次の様に表現すると、
| y1=sin(2π |
1 |
t) |
(1) |
| T1 |
| y2=sin(2π |
1 |
t) |
|
| T2 |
|
y1,y2:規則波の水位,T1,T2:規則波の周期,t:時間,π:円周率
|
2つの規則波の合成波は次のように書ける。
| y= |
y1+y2= |
sin(2π |
1 |
t) |
+sin(2π |
1 |
t) |
(2) |
| T1 |
T2 |
また、三角関数の加法定理を用いると(2)式は次のように変形できる。
| y= |
2sin(2π |
T1+T2 |
t)・cos(2π |
T2-T1 |
t) |
(3) |
| 2T1T2 |
2T1T2 |
(3)式における2つの項をA項とB項とすると、周期の長い項はB項である。
| A=sin(2π |
T1+T2 |
t) |
B=cos(2π |
T2-T1 |
t) |
| 2T1T2 |
2T1T2 |
従って、合成波(y)の振幅が最大になる時間間隔(うなりの周期)をTBと
すると、(3)式のB項の絶対値が最大になり、再び最大になるまでの時間
がTBであることが分かる。つまり、ある時刻t=t0に振幅が最大になり、
t=t0+TBに再び振幅が最大になる。従って、次の関係が成立する。
| 2π |
T2-T1 |
(t0+TB) - 2π |
T2-T1 |
t0=π |
(4) |
| 2T1T2 |
2T1T2 |
(4)式を整理するとビート周期(TB)は次のようになる。
|